Whitening Filter
Usually, we need to filter a mixture of desired signal and colored noise, in order to make the spectrum of the noise become white.
Without loss of generality, \(x(t)\) is a wide-sense stationary stochastic process. If it is taken as input by a linear time invariant (LTI) system \(W\) and the output process \(n(t)\) has white power spectrum, i.e., power spectrum density (PSD) equal to 1; then the system \(W\) is termed the whitening filter of process \(x(t)\), and \(n(t)\) is termed the innovation process of \(x(t)\). If \(n(t)\) is input into the inverse system of \(W\), denoted by \(W^{-1}\), then the output is the original process \(x(t)\) and system \(W^{-1}\) is the corresponding innovation fitler, as shown in Figure 1.
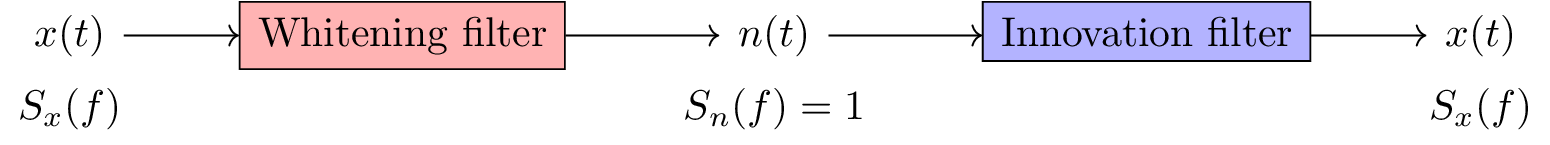
Figure 1: Whitening filter and innovation filter
Providing a multidimensional stochastic vector \(\mathbf{x}\) with covariance \(\mathrm{Var}[\mathbf{x}] = \mathrm{E} \left[ \mathbf{x} \mathbf{x}^H\right]\), if its whitening filter is denoted by \(\mathbf{H}\), then its output \(\mathbf{y} = \mathbf{Hx}\) should have unit covariance, i.e.,
\begin{align*} \mathrm{Var}[\mathbf{y}] &= \mathrm{E} \left[ \mathbf{y} \mathbf{y}^H\right] \\ &= \mathrm{E} \left[ \mathbf{Hx} \mathbf{x}^H \mathbf{H}^H \right] \\ &= \mathbf{I}. \end{align*}Clearly, the equation above holds if and only if \(\mathbf{H} = \mathbf{L}^{-1}\), where \(\mathbf{L}\mathbf{L}^H = \mathrm{Var}[\mathbf{x}]\).