Uniform Distribution in a Ring Area
This post aims to provide an efficient method of generating uniformly distributed coordinates in a given ring area.
Without loss of generality, the ring area is illustrated in Figure 1. The inner and outer radii are \(R_1\) and \(R_2\), respectively, \(R_1 < R_2\). The corresponding angular scope starts from \(\Theta_1\) and ends at \(\Theta_2\), \(\Theta_1 < \Theta_2\).
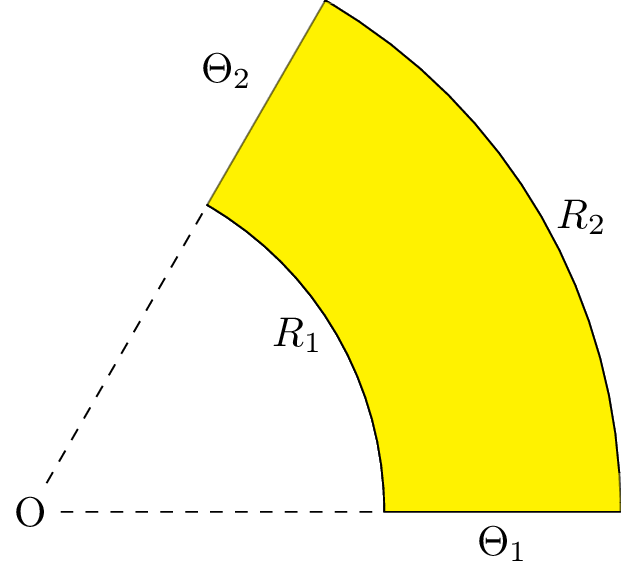
Figure 1: A ring area
In polar coordinate system, the joint probability density function (PDF) of the radius and angle can be written as
\begin{align*} f_{R, \Theta}(r, \theta) = \frac{2r}{(\Theta_2 - \Theta_1)(R_2^2 - R_1^2)}, \end{align*}where \(\theta\in[\Theta_1, \Theta_2]\), \(r\in[R_1, R_2]\).
Then, the PDFs of the radius and angle can be expressed as
\begin{align*} f_R(r) &= \frac{2r}{R_2^2 - R_1^2}, \quad r\in[R_1, R_2];\\ f_{\Theta}(\theta) &= \frac{1}{\Theta_2 - \Theta_1}, \quad \theta\in[\Theta_1, \Theta_2]. \end{align*}Consequently, the target coordinate can be generated as follows
- A desired radius can be got by \(\sqrt{XR_1^2 + (1-X)R_2^2}\), where \(X \sim \mathcal{U}(0, 1)\).
- A desired angle is uniformly distributed within the range \((\Theta_1, \Theta_2)\), i.e., \(\Theta \sim \mathcal{U}(\Theta_1, \Theta_2)\).